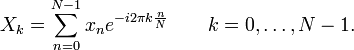...or at least I hope I can explain it understandably. I've wanted to know how to do the fast fourier transfor forever, but despite reading many descriptions of it, I always ran in to one problem: Smart people suck. A lot.
Some of it has to do with them really not being that smart. There's a set of people who enjoy the idea that they are smart, and so believe that they know things that they don't really understand, and when you search for information about something and find one of their explanations, you end up reading something that makes no sense and often just ignores the more complex aspects, which are obviously the parts you need the most help with.
The rest of it comes from what I can only assume is some attempt by the smart people to show off their smarts. They'll often explain the simpler parts in excessive detail, but then be as concise as possible with the more complex parts, utilizing every bit of advanced bullshit they know, seemingly just to show off that they know it.
I suppose I could be wrong, but then where else does shit like this come from?
Image from Wikipedia's "Fast Fourier Transform" page.Ooh, look! Someone knows maths!
One sure sign that your description sucks is when someone who already knows how to do what you're describing can't even understand it. I've known how to do slow Fourier transforms for years. I had to figure out on my own how to do them as I never found a decent explanation of how they work. Even after I knew how to do them, I still saw equations like the above and could think nothing other than "what the fuck?" It wasn't until Wolfram Alpha explained what the "e ^ (-i * 2 * pi)" meant that I had any idea how the above formula had anything at all to do with what I already knew how to do. It's a neat mathematical trick I suppose, and certainly useful when creating a concise statement of the algorithm, but when you're trying to explain something to someone who doesn't already know it, concise isn't what you want.
So, having finally figured out how the fast Fourier transform works, (and, again, with no help from the smart people of the world, but rather, I just sat down and figured it out on my own), I feel the need to explain in simple understandable terms how it works.
Hopefully I've accomplished that as I've now spent enough hours writing this that I'm no longer sure I care.
Step 1: The slow Fourier transform.
Since the fast Fourier transform is an optimization of the slow Fourier transform, I should first explain how that works.
I first discovered how to do this while reading an electronics textbook about radio communications. I was reading about how to "mix" the antenna signal with a frequency in order to shift the radio frequencies down to audio frequencies. ...but nevermind all that.
The important thing I learned from this book is that if you have two sine waves of frequencies A and B, and you multiply the waveforms together, the resulting waveform is the sum of the frequencies A+B and A-B.
At first I found this difficult to believe, and so I wrote some QuickBASIC programs to verify it. However, in the age of Wolfram Alpha, verifying such things is as simple as clicking a link:
2 * cos(a*x) * cos(b*x) = cos((a + b) * x) + cos((a - b) * x) Still, a result of "true" doesn't do justice to just how amazing it is.
In writing those QuickBASIC programs, I quickly realized that I could use this property of sine waves to figure out how much of a frequency was in an input signal. By multiplying the input waveform by the frequency I wanted to look for, that frequency would be shifted to 0 Hz, turning it into a DC offset. I could then average the signal over the sample period, and that average would represent to what degree that frequency was present.
The only problem was that the resulting DC offset depended on the phase difference between the frequency as it existed in the input signal, and the frequency I was multiplying. If they were both the same phase, the DC offset was at its maximum, but if they were 90 degrees out of phase, the DC offset was zero. To solve this, I simply performed the operation twice, once using sin() and another using cos(), and thus one of those was guaranteed to produce a non-zero average. I then found that treating the two resulting values as an (x, y) coordinate, and finding the distance from origin (which is sqrt(x*x+y*y) if you didn't already know), gave a result that was constant regardless of the phase of the input signal. Also, the angle of (x, y) represented the phase of the frequency in the input.
To sum all of that up in some C code:
float x = 0;
float y = 0;
for (int i = 0; i < SAMPLE_COUNT; i++) {
x += sample[i] * cos(2 * M_PI * frequency * i / SAMPLE_RATE);
y += sample[i] * sin(2 * M_PI * frequency * i / SAMPLE_RATE);
};
x /= 0.5 * SAMPLE_COUNT;
y /= 0.5 * SAMPLE_COUNT;
float magnitude = sqrt(x * x + y * y);
float angle = atan2(y, x);
You'll likely want to do it multiple times for several frequencies, but that's the basic idea.
There is a lot more to it, however. For example, it's mathematically the case that the only frequencies it makes sense to look for are those given by this code:
for (float f = 0.0; f <= SAMPLE_RATE / 2; f += SAMPLE_RATE / SAMPLE_COUNT) {Frequencies above SAMPLE_RATE / 2 simply aren't present in the data, and while you can test for more than the steps of SAMPLE_RATE / SAMPLE_COUNT, the resulting data isn't any more accurate. Basically it's a matter that there's only so much input data and so you're only going to get so much output data.
Step 2: The Fast Fourier Transform
The key to understanding the fast Fourier transform came to me when, while reading a PDF about it written by some moron, it occurred to me that it couldn't be anything other than just an optimization of the above. So at that point I decided "fuck everyone else and their incomprehensible explanations" and instead focused on figuring out how to do it on my own. I should have done that years ago as it only took a day of thinking about the problem to figure it out.
The first obvious optimization is to realize that only certain sine/cosine values are used. You can create an array of just the values for the lowest frequency, then step through that array twice as a fast for the next frequency, then 3 times as fast for the third frequency, etc. However, that doesn't address the O(n^2) complexity of the problem, and thus has nothing to do with fast Fourier transforms.
So I wrote out the steps for a small transform of eight data points, figuring that if I could find an optimization there, then I could extrapolate that to larger data sets.
A transform of eight data points (assume eight samples of data at eight samples/second) involves summing each of the eight samples multiplied by the cos/sin values for that frequency. Here are the operations in table form:
| Frequency | Sample 0 | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | Sample 6 | Sample 7 |
|---|
| cos 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|
| sin 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
| cos 1 | 1 | 0.7071 | 0 | -0.7071 | -1 | -0.7071 | 0 | 0.7071 |
|---|
| sin 1 | 0 | 0.7071 | 1 | 0.7071 | 0 | -0.7071 | -1 | -0.7071 |
|---|
| cos 2 | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
|---|
| sin 2 | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 |
|---|
| cos 3 | 1 | -0.7071 | 0 | 0.7071 | -1 | 0.7071 | 0 | -0.7071 |
|---|
| sin 3 | 0 | 0.7071 | -1 | 0.7071 | 0 | -0.7071 | 1 | -0.7071 |
|---|
| cos 4 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
|---|
| sin 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
For the frequency zero (the DC offset) you just sum all eight samples (and divide by eight afterwards). This is because the cosine of zero is one, and the sine is zero, thus the coefficients are always one and zero.
For frequency one, the values are more complex, but the calculation is the same: multiply each sample by the coefficient, then sum the results, and divide by eight. Then you have two sums, one for cos and one for sin, which like above create a vector whose magnitude represents the amplitude and angle represents the phase of the frequency.
The first obvious thing that stands out is all of the coefficients which are just zeros and ones. However, accounting for them isn't a useful optimization because there is only so many of them because of the small sample size. Larger sample sizes contain far fewer of them. Smaller sample sizes contain nothing but ones and zeros.
So I stared at this for some hours until I started to wonder what exactly I was getting by including the odd-numbered samples when calculating the value for frequency one. I can calculate a value for that frequency using only the odd samples or only the even samples. So why not just leave out the odd samples and save myself the trouble? What was I getting by including them in the calculation that I wouldn't get without including them?
Then I realized that what including the odd samples gets me is the ability to distinguish frequency 1 from frequency 3. Without them, if I have frequency 3 in the sample, it triggers a result for frequency 1.
Then it occurred to me that by calculating the transforms for the even and odd samples separately, I could combine the two results like this:
cos 0 = even 0 + odd 0
cos 1 = even 1 + odd 1
cos 2 was completely different
cos 3 = even 1 - odd 1
cos 4 = even 0 - odd 0
The sin sums could be calculated similarly, except for the sin sum for frequency 3. The odd sum was there unmodified, but the even sum was different.
Then it occurred to me that the values for cos 3 weren't simply copied from the values for cos 1, but rather, the values were the result of a rotation of that vector, and it just happened that the rotations were such that the values were quite similar.
The value for sample 0 was copied unmodified.
The value for sample 1 was rotated 90 degrees, which results in the negative value for the cos sum, but results in the same value for the sin sum.
The value for sample 2 was rotated 180 degrees, which results in the same value for the cos sum, but the negative value for the sin sum.
The value for sample 3 was rotated 270 degrees, which results in the negative value for the cos sum, but results in the same value for the sin sum.
Samples 4 through 7 follow the same pattern.
At this point, I realized it would probably do me a lot of good to look at the problem in terms of complex numbers, and so I scrapped the page and started a new one.
If you don't know what complex numbers are, here's a quick tutorial:
Basically, each complex number is composed of two normal numbers. One, the "real" component, is like any other number. The other component, called the "imaginary" part, is defined by the special constant "i" which has the unique property that multiplying it by itself results in the value of -1. Now, if you know how to multiply, you know that there are no numbers that when multiplied by themselves result in a negative number, but that's why it's called "imaginary." These numbers are usually expressed in the form of "a + bi" where "a" is the real part and "b" is the imaginary part. An alternative syntax is to represent them as an (x, y) coordinate, with x being the real component and y being the imaginary component.
Adding two such numbers, such as "a + bi" and "c + di" simply results in "(a+b) + (c+d)i", or in other words, you just add together the two real parts, then separately add together the two imaginary parts. The resulting vector is the point you get when you take the segment from (0, 0) to (a, b) and stick it on the end of (c, d). If (a, b) is (1, 0) and (c, d) is (0, 1) then the new vector is (1, 1).
Multiplying two such numbers is particularly interesting. To multiply them, you simply use "distribution" which you learned in algebra class. (a + bi) * (c + di) = (a * b) + (a * di) + (c * bi) + (bi * di), and since i multiplied by itself turns into -1, the (bi * di) at the end turns into simply -(b * d). Thus the real component is (a * c) - (b * d), and the imaginary component is (a * d) + (b * c).
Why complex numbers are useful in this case is that the provide a simple way to rotate vectors. To rotate a vector by an angle, all you have to do is express it as a complex number, then multiply it by a vector of length one at the angle you want to rotate the first vector by.
For a simple example, consider if you have (1, 0) and you want to rotate it 90 degrees. To calculate the unit length vector for 90 degrees, just calculate (cos(90), sin(90)), which happens to be (0, 1) which makes this an easy example. When you multiply (1, 0) by (0, 1) the result is (0, 1). Then you multiply again, and now the result is (-1, 0). Then you multiply again, and now the result is (0, -1). Finally, if you multiply again, you're back to (1, 0), as four times 90 degrees is a full circle.
This works no matter what angle you use. For a more complex example, consider 45 degrees, whose unit length vector is (0.7071, 0.7071). (which is (cos(45), sin(45)). If you multiply that by itself (thus rotating a 45 degree vector by 45 degrees) you get this result:
real = 0.7071 * 0.7071 - 0.7071 * 0.7071 = 0
imaginary = 0.7071 * 0.7071 + 0.7071 * 0.7071 = 1
Which is (0, 1) which is the 90 degree angle.
So, let's rewrite the table from above, but now we'll assume that we are dealing with complex numbers. Obviously our eight samples won't have imaginary parts, but now rather than calculate two sums, we calculate just one which contains both the cosine and sine sums as real and imaginary parts. Also, rather than put the complex number representing each angle in each box, I'll just put a single digit, which is the index into the array of cosine/sine values (which I'll explain a bit more below).
| Frequency | Sample 0 | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 | Sample 6 | Sample 7 |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| 2 | 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 |
|---|
| 3 | 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 |
|---|
| 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 |
|---|
| 5 | 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 |
|---|
| 6 | 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 |
|---|
| 7 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|
Note that we now go up to frequency 7, which we're allowed to do. It was only limited to frequency 4 before because, without the cosine data in our input, frequencies 5 through 7 end up being a mirror of frequencies 3 through 1. However, I've chosen to "abstract" the problem to the "general" case of a transform of complex values, thus we do all eight frequencies now.
Since all of our frequencies are a multiple of frequency 1, we only need a table of the values for frequency 1, of which there are eight, one for each sample. Then for frequency 2, we just step through the array twice as fast, and once we reach the end, we wrap to the beginning again. For frequency 3, we step by threes. Thus there are only eight values we ever multiply any of the samples by.
So, again, let's look at how we might combine the results of two separate transforms, one of the even samples and a another of the odd samples. To make that comparison simpler, I'll make two separate tables for those two transforms:
| Transform A | Transform B |
|---|
| Frequency | Sample 0 | Sample 2 | Sample 4 | Sample 6 |
|---|
| 0 | 0 | 0 | 0 | 0 |
|---|
| 1 | 0 | 2 | 4 | 6 |
|---|
| 2 | 0 | 4 | 0 | 4 |
|---|
| 3 | 0 | 6 | 4 | 2 |
|---|
| | Frequency | Sample 1 | Sample 3 | Sample 5 | Sample 7 |
|---|
| 0 | 0 | 0 | 0 | 0 |
|---|
| 1 | 0 | 2 | 4 | 6 |
|---|
| 2 | 0 | 4 | 0 | 4 |
|---|
| 3 | 0 | 6 | 4 | 2 |
|---|
|
Obviously the result for frequency zero is just the sum of the result for 0 from each of the two separate transforms. The results for the other three can be calculated like so:
Frequency 1: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 1.
Frequency 2: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 2.
Frequency 3: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 3.
At this point we haven't really saved any time. We're doing just as many calculations, just in a different order. Where we save time comes from re-using the above values to calculate the next four frequencies.
Frequency 4: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 4.
Frequency 5: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 5.
Frequency 6: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 6.
Frequency 7: take the result from transform A, and add to it the result from transform B, advanced in phase by angle 7.
If you draw out a similar reduction of the two tables above into four smaller transforms, a pattern becomes apparent:
1. The values in the combined transform always come from the values in the smaller transform in the same pattern: The first frequency's value always comes from the first values in the two smaller transforms. The second result always comes from the second values. Also, like above, the second (new) set of frequencies in the result is always re-uses the first set of values in the same way.
2. The angle by which the second set needs to be advanced is equal to the difference in angle between the two sets multiplied by the frequency. Thus, above, it was always just the frequency itself. In the second recursion, however, the difference in angle between the two transforms is twice as large, thus then phase adjustment is twice as large.
Thus, the idea is simple and the patterns are simple, and so there's no reason why people need to make it seem so difficult. Even the math is simple enough if you take the time to explain it.
Step 3: Implementation
I wrote
some code to implement this algorithm. It isn't very self-explanatory, so I'll explain how I implemented it here.
First thing to notice is that C99 includes a complex data type. Type "man complex" in Linux to learn about it. Thus, rather than manage cosine/sine or real/imaginary values manually, I just used the standard data type.
The first thing to do is to calculate the cosine/sine values and store them into a table. To do that, I use code like this:
for (int i = 0; i < samples; i++) {
table[i] = cexp(-2 * M_PI * I * i / samples);
};This is similar to the "e ^ (-2 * pi * i * n / N)" in the formula above that I copied from Wikipedia. Turns out this nonsense is a simple way to get the cosine/sine pair as a complex number. The "k" term is left out, since we include it when we index into this array.
To implement the transform, I decided to write a function which takes five arguments. Two are pointers to an input/output array, "temp" and "data" below, but exactly which is the input and which is the output is complicated. The third argument is an index into the sample data. The fourth is a step size. The fifth is the number of samples to be transformed.
if (count > 2) {
recursive(temp, offset, step << 1, count >> 1, data);
recursive(temp, offset + step, step << 1, count >> 1, data);
};To split the transform into two smaller transforms is rather simple. The first has the same offset, but the step size is doubled, while the count is halved. The second is similar, except that the offset is incremented by the step size. This recursion is continued until there are only two samples to be transformed. The transformation of a single sample is just that sample itself. Thus there's no reason to call the functions in that case since they would simply return their original value.
Then to combine the two transforms, I use this code:
for (int i = 0; i < count >> 1; i++) {
int a = offset + step * i;
int b = offset + step * (2 * i);
int c = offset + step * (2 * i + 1);
int d = (step * i) & (samples - 1);
data[a] = temp[b] + temp[c] * table[d];
};
for (int i = 0; i < count >> 1; i++) {
int a = offset + step * (i + (count >> 1));
int b = offset + step * (2 * i);
int c = offset + step * (2 * i + 1);
int d = (step * (i + (count >> 1))) & (samples - 1);
data[a] = temp[b] + temp[c] * table[d];
};The two for() loops handle the first and second halves of the frequency range.
Variable "a" calculates the index into the array we store our results into. Thus it is the offset we were given, incremented by the step size for each subsequent result. the second for() loop's equation adds half of the count to this, since it's doing the second half of the frequencies.
Variables "b" and "c" calculate the index into the results from the first and second transforms, which is why the "i" is multiplied by two (each transform processed every other value) and "c" is offset by 1.
Variable "d" calculates the offset into the table of cosine/sine values in complex number format. Again, "count >> 1" is added in the second for() loop in order to cover the higher range. The result is then clipped so that it doesn't overflow the array, so that the index values just wrap around the array as necessary.
Finally, since C99 has that complex data type, the actual math is rather simple.
data[a] = temp[b] + temp[c] * table[d];
All of the values are complex numbers, thus what the C compiler generates is actually four multiplies and four additions.
There are obviously many ways this could be optimized. I haven't bothered since, short of keeping the cosine/sine values in a table, nothing makes as much of a difference as simply using a fast transform vs. a slow one.
However, were I to decide I needed to, the most obvious approach I can think of is to add "printf()" statements that output the operations as a long list of C code, then simply let GCC optimize it. With all of the values printed out, GCC would easily see where all of those multiplies by zero or one are and optimize them away and it would certainly figure out how best to use the FPU stack to avoid unnecessarily storing values to memory. If I included the code that converts my data into complex numbers, it would likely even find optimizations that result from the excess of zero imaginary parts in the input data.
As for which of the "data" and "temp" are input and output, there's a fun story behind that...
It started with me trying to optimize a merge sort I'd written. The merge sort works in a similar way, dividing its input into two halves, then calling itself to sort each half, then simply merging the two sorted halves, which is an easier problem to solve.
At first it would take the input data, pass it to itself to sort the two halves, then copy that data to a temporary workspace so that it could overwrite the original data when sorting the data out of the temporary space. Thus there was a full copy of the data for each recursion, and it occurred to me that eliminating that would save some time.
So I thought that if I just changed the function so that, rather than sorting the data in place, it sorted it into a new buffer, the problem would be solved. So I changed the function's arguments to require separate input and output buffers.
This created a problem, however, due to the fact that the function calls itself. I now had to change those calls to also use separate input and output buffers. So those calls now moved the data from the input buffer to the output buffer, which again meant that I had to move it back to the input buffer before I could merge the lists into the output buffer.
Unfortunately I didn't figure that out so easily. I must have rewritten the function ten times, confusing the hell out of myself since it seemed obvious there must be some way to do this without needlessly copying the data for each recursion, but when I changed the function to require separate input/output buffers, it needed to call the function it was before when it sorted into the same buffer, but when I changed it back to that, it now needed a function that used separate input/output buffers.
So I solved this problem with copy & paste. I made two copies of the function, one which takes the data in one buffer and returns it in the other, and the other which takes the data in the output buffer, sorts it, and simply uses the input buffer as scratch space. Each function called the other recursively. Finally it did what it was supposed to.
This was the code which I decided to rewrite in assembly to see if I could beat the compiler's code.
So after writing one version of the code in assembly, I decided to diff the two functions to see what exactly I had to change. Turns out the two functions contained only one difference: The function that sorts in place would return immediately when asked to sort one item, whereas the function that used separate input/output buffers first copied that single item to the output buffer, then returned. Other than that, the two functions were identical.
This prompted me to test the hell out of the two functions to verify they did what I thought they did. ...and indeed they did. Calling "sort_yes_move" would sort the data in its second argument and return it in its first, and calling "sort_no_move" would sort the data in its first argument and return it in the same place. ...and yet the two functions differed only via that one line of code.
I must have thought about this in the back of my mind for a day before I finally figured out why it worked.
Basically, since each recursion of the function moves the data from one buffer to the other, which buffer it needs to be in to begin with depends on whether the recursion depth is odd or even. Since the functions call each other, that tracks the odd/even depth, and the statement to copy the data from the one buffer to the other in the one function takes care of copying it before anything is done. The functions also inverted the order of their two arguments when calling each other, so that each one read the data written into the opposite buffer by the other. Thus, which function I called first determined which buffer was considered input and which was considered output and also determined whether it was an even or odd recursion depth that required the data to be moved first.
In my FFT code, I encountered the same problem: When merging the two sets of data, I needed to preserve the results from the recursive calls while calculating the results of the current step. So I did the same thing, making the recursive calls reverse the order of the two buffers. However, rather than use two copies of the function, I instead just used one, and took care of copying the data to the correct buffer before calling the recursive function:
if ((int) trunc(log(samples) / log(2) + 0.5) & 1) {
memmove(temp, input, samples * sizeof(complex));
} else {
memmove(data, input, samples * sizeof(complex));
};The formula there just figures out whether the number of samples is an even or odd power of two, which determines whether there will be an even or odd number of recursive steps, and thus, which of the two buffers will be the first one to be read from. It then copies the data into that buffer. (An alternate method would be to always copy the data to the same buffer, but to call the recursive function with the "data" and "temp" parameters in a different order for each of the two cases, and then copy the data from the correct pointer afterwards.) (...or, as another alternative, you could just copy it to both arrays...)
So, in the event anyone reads all of that and now understands the Fast Fourier Transform despite not previously understanding it, please let me know that I've accomplished my goal and I'll turn this into something more permanent than a blog post.
0-100