This article is a conversation that occurred in my Discord server when I was trying to figure out how to process 3-Axis gyroscope data properly. Being a conversation between two people, it's not exactly a blog article, but the information was hard to find, so I want to try to put it on the internet anyway and the conversation surrounding it might be good Google bait for similar questions.

In the future, I'd like to do a better write-up of the code I ended up with, but for now, this is better than nothing for someone who is looking for this information.

Octapoo

I don't suppose anyone knows anything about integrating 3 axis gyroscope data? Unfortunately all that the internet is willing to tell me is how to integrate a single axis, even when I search for "3 axis" because everyone trying to integrate a single axis is using a 3 axis gyroscope anyway.

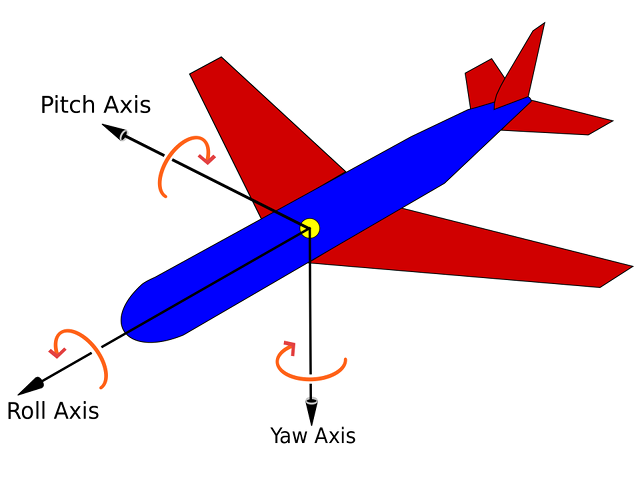
The problem I have is that if the gyroscope tells me that I've rotated 90° on the pitch axis and the roll axis simultaneously, then how do I apply that to the plane's current orientation to find its new orientation? If I apply the pitch axis rotation first, then the roll axis rotation, I end up with the nose and tail of the plane oriented up and down, but if I apply the roll axis rotation first, then the pitch axis rotation, I end up with the wings oriented up and down.

Obviously what actually happened to make the gyroscope return those readings is between those two positions, and at least for the case of two axes I think I know what it means, that the rotation actually occurred on an axis between the pitch and roll axis.

However, what if it tells me that I've rotated 90° on all three axes? I can't even begin to imagine what that means. In the case of two axes, they share a common plane, and so it makes sense that the actual axis of rotation is on that plane too, but in the case of all 3 axes, they don't share a common plane, so the approach that I think works for 2 axes cannot work for 3 axes.

@Big Yoshi I feel like this is something you might know.

Big Yoshi

how do you end up with two different orientations

Octapoo

Say that the nose/tail are presently on the X axis, the wings are on the Y axis, and the top/bottom of the plane are on the Z axis.

If you do the pitch first, then the plane rotates on the Y axis so that the nose/tail are then on the Z axis. Then when you do the roll, the nose and tail remain on the Z axis, and the wings rotate from being on the Y axis to being on the X axis.

If you do the roll first, then the plane rotates on the X axis so that the wings are on the Z axis. Then when you do the pitch, the wings remain on the Z axis and the nose/tail rotate from being on the X axis to being on the Y axis.

Big Yoshi

ahh i see

how do the rotations happen simultaneously

Octapoo

Well, I figured that in the case of two axes that it would happen if I rotated it on an axis between the X and Y axis, and that if I made a full rotation then the gyroscope would report sqrt(2) * 360° of rotation on each axis, which is about 255°. So I tried this out with the gyroscope and it does indeed indicate approximately that much rotation on each axis, though there's enough imprecision both in cumulative errors and in me just not being able to rotate the thing perfectly that I can't be certain that's correct.

However, that solution I figured because if there's only two axes of motion then the actual axis of motion is probably between those two, on the same plane. So I just figured, add them up like a vector, and there's only one line that's perpendicular to that vector that is also on the plane of those two axes, and so that must be the line that the rotation occurs around. (maybe I didn't actually do the math here so maybe that logic is bunk)

However, with 3 readings from 3 perpendicular axes, there is no common plane, so after I add up the 3 measurements like a vector, there's a whole slew of possible lines that are perpendicular to that vector and thus no way to determine what axis the rotation occurs around.

I don't know that the gyroscope will actually give readings on all 3 axes at once, but I figure it must since it's possible to rotate the thing on an axis that isn't on the plane of any two of the three axes that it senses.

Playing with it right now, it's a little tricky but it is possible to move it such that all 3 axes report movement at once. I'm not quite sure what I'm doing to make it happen though.

Big Yoshi

haha that sounds fun to try to do

Octapoo

So far my only idea is something like this:

However, I want to do this on an ATmega328 to put it on my RC plane to make it able to fly itself, and I think doing each calculation a thousand times is probably asking too much of that microcontroller.

What I need is a solution that's like "as that 1000 approaches infinity..."

Big Yoshi

so like

a rate of change maybe

Octapoo

Well, the readings from the gyroscope are a rate of change. It tells me how many degrees per second it is sensing on each of its 3 axes.

So far this video is the only thing I've come across that even begins to approach the problem, starting at time offset 9:55 in the video.

However, he ignores the problem of applying the 3 rotations simultaneously and just does them in order, which is close to the same if the rate of rotation is small, but the faster the rotation, the more significant the error. He also doesn't even calculate all 3 rotations.

I was surprised at how accurate the readings he gets are, which is what made me start looking into it, as the gyroscope I bought from eBay a couple of years ago happens to be the same one he's using in the video.

Big Yoshi

hmm interesting

maybe you also need an accelerometer?

Octapoo

It has an accelerometer in it too, which he uses in the part 2 of that video to correct for the drift that occurs due to cumulative errors. Obviously I need to do that too, but I'm imagining that if the plane rotates at a rate of one rotation per second, then at the 50 Hz sampling rate, each reading will indicate 7.2° of rotation, which seems large enough that the errors that occur from calculating the X,Y,Z rotations in order rather than simultaneously will add up rather quickly.

Big Yoshi

yea you might need more sampling

Octapoo

Yes, that's kind of the idea of processing each reading in 1000 steps, except that I probably don't need to actually do 1000 steps to get it close enough. IDK, I'd just rather do it correctly if I can figure out how.

I might just need to write some code for my 1000 steps approach, and see if I can play around with the inputs and watch how the outputs change and see something that makes the correct formula obvious. ...but I'm not looking forward to that because it's easy to imagine not discovering anything from it.

Big Yoshi

well

i guess from your original question, rotating in different axis order does give you a different position

but if you combine that with the accelerometer, pitch first then roll will give you gravity in the X direction

and roll first then pitch gives it to you in the Y direction

i think

so combining those two readings would tell you how the plane is oriented

or how it is orienting

Octapoo

The accelerometer can tell you which way is down, but it can't account for yaw rotation, and it also measures acceleration that isn't due to gravity and so which way it points isn't always down. In the second video to the one I posted, he takes the accelerometer data and uses a low-pass filter to kind of filter out the accelerations that aren't due to gravity, and uses the result of that as a slight adjustment to the orientation to cancel out the drift that occurs due to cumulative errors in adding together the gyroscope readings. That's a long-term solution that can account for drift, but it doesn't do anything for the short term problem of knowing the orientation at the present moment.

Trying to use the accelerometer was actually the first thing I tried when I got this thing, but I then quickly figured out that it points the wrong way when I accelerate it, and figured I probably needed to use the gyroscope to correct it somehow, but never looked into it further as it wasn't obvious to me how to proceed. Then I saw that video and realized I'm supposed to use the gyroscope primarily and use the accelerometer to correct it.

Second video link BTW:

Big Yoshi

hmmm damn i remember doing these rotation matricies

but i just remember that the order matters haha

Octapoo

I've done them before too. Once MME allowed you to turn in all directions, even up-side-down, so it was doing this sort of thing. However, I just applied the control inputs in some order, and since it was just a game and it didn't matter, it wasn't apparent that anything was wrong.

Big Yoshi

this sounds like what you're looking for

https://www.researchgate.net/publication/51873567

Octapoo

I could just be imagining a bigger problem here than I'll actually have. I should probably write some code that compares applying the rotations in some order to the "correct" answer achieved by dividing the calculation into 1000 steps and from that calculate what the actual error is.

That is a promising-sounding title.

Very promising...

Now this is something I've been wondering about. IDK if you remember but I was once talking to you about a space movie where they were dealing with some rotating satellite and fucked something up and someone said "it was rotating on one axis but now it's rotating on all three" and I thought it was stupid because I didn't think it was possible to rotate on 3 axes. Then, I don't remember if you brought it up or if I found it somewhere, but there's the problem of how an object can spin on its axis of greatest rotational inertia or its axis of least rotational inertia, but not on any other axis. ...and so I was thinking the odd wobbling was 3-axis rotation, and maybe that's what the script-writers meant, but in trying to figure this out I wasn't so sure that 3 axis rotation was possible anymore. Like maybe that's more of a problem of the momentum constantly oscillating between different parts of the object.

IDK, that's not too important just something I was thinking about.

Big Yoshi

haha that's the first thing i thought of

Octapoo

I found a video of a simulation (looked like a video game) of that same shape. It's cool to see it actually happen in real life.

Big Yoshi

something about spinning on its intermediate axis

Octapoo

This paper seems to be 100% what I'm looking for.

Big Yoshi

oh nice

that second part was what i was thinking

you too but with 1000

Octapoo

It's interesting to read papers and see people come up with terms like "iterative infinitesimal rotation approximation" and just be like "yeah, that's a nice concise way to explain that."

Big Yoshi

i like how the title sounded very complicated

and when i read it i was all "hey i know what this means"

Octapoo

I have a real fear of greek letters. They usually lead to me not understanding stuff.

That's an interesting insight at least. Basically it's saying that if I do cut the rotation into 1000 steps, each of those 1000 steps is the same angle of rotation, and thus if I were to simply calculate one very small step it would tell me the correct angle of rotation.

So I guess the answer is just this, if I'm reading it correctly:

I felt like sqrt(x² + y² + z²) would be involved but it was nothing more than a guess. Also I'm not good with matrix multiplication, but I can only think of one thing that multiplying a single value by a matrix is going to do, so overall this looks quite easy. I'll give it a try and see if it works.

Octapoo

@Big Yoshi

Big Yoshi

nice it works!